Answer: 1.57
Step-by-step explanation:
This described situation is known as Refraction, a phenomenon in which light bends or changes its direction when passing through a medium with a index of refraction different from the other medium.
In this context, the index of refraction is a number that describes how fast light propagates through a medium or material.
According to Snell’s Law:
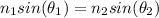 (1)
(1)
Where:
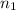 is the first medium index of refraction (the value we want to know)
is the first medium index of refraction (the value we want to know)
 is the second medium index of refraction (air)
is the second medium index of refraction (air)
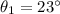 is the angle of incidence
is the angle of incidence
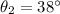 is the angle of refraction
is the angle of refraction
Now, let's find
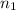 from (1):
from (1):
 (2)
(2)
Substituting the known values:
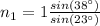
Finally:
