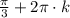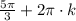Question

Solve the given equation. (Enter your answers as a comma-separated list. Let k be any integer. Round terms to two decimal places where appropriate.)

cos(θ) = 1/2

Answer 1

That is the solutions are:

`(\pi)/(3)+2\pi \cdot k`,
`(5\pi)/(3)+2\pi \cdot k`

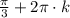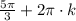
Explanation:

The period of
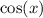`\cos(x)` or
`\sin(x)` is
`2\pi`.

Let's look at the first rotation to see when
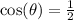`\cos(\theta)=(1)/(2)` happens.

This happens at
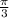`(\pi)/(3)` and also at
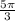`(5\pi)/(3)`. (Notice I just looked at the x-coordinates because that is what cosine is. Sine is the y-coordinate.)

Now to find the rest of the solutions we can just make full rotations either way to get back to those points .

That is the solutions are:

`(\pi)/(3)+2\pi \cdot k`

`(5\pi)/(3)+2\pi \cdot k`