Answer: It remains the same
Step-by-step explanation:
The Conservation of Momentum principle establishes that the initial momentum
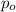 must be equal to the final momentum
must be equal to the final momentum
 :
:
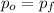 (1)
(1)
In the case of the train, its initial momentum is:
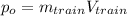 (2)
(2)
Where
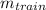 is the mass of the train and
is the mass of the train and
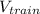 is the initial velocity of the train
is the initial velocity of the train
And, its final momentum is:
 (3)
(3)
Where:
 since we are told the mass of the train is doubled
since we are told the mass of the train is doubled
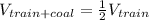 since we are told the velocity of the train goes to half
since we are told the velocity of the train goes to half
Hence:
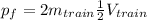 (4)
(4)
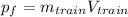 (5)
(5)
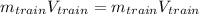 (6)
(6)
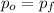
This means the momentum of the train remains the same.