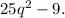Question

The side lengths of a square are each 5q. By adding 3 to the length and subtracting 3 from the width, a rectangle is made. What is the area of the rectangle?

Answer 1

5 becuz u gotta do the work

Explanation:

5+3=8

8-3=5

Answer 2

The area of the rectangle is
`25q^2 - 9.`

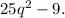
To solve this problem

In this case, the length of one side is 5q, so the area of the square is
`(5q) * (5q) = 25q^2.`

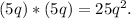
A rectangle is created by increasing the length by three and decreasing the width by three. Accordingly, the rectangle's new length is
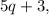`5q + 3,` and its new width is
`5q - 3.`

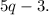
Multiplying the length by the width yields the area of a rectangle. The length in this instance is 5q + 3, and the breadth is 5q - 3. Thus, the rectangle's area is
`(5q + 3) * (5q - 3).`

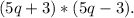
Now, let's simplify the expression. We can use the distributive property to expand the equation:

`(5q + 3) * (5q - 3) = (5q * 5q) + (5q * -3) + (3 * 5q) + (3 * -3)`

=
`25q^2 - 15q + 15q - 9`

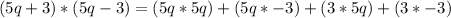
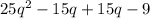
Observe that because the middle terms have opposing signs, they cancel each other out
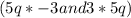`(5q * -3 and 3 * 5q)`. In a similar vein, the final terms
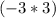`(-3 * 3)` reduce to -9.

The equation simplifies to:

`25q^2 - 9`

Therefore, the area of the rectangle is
`25q^2 - 9.`