Question

F(x)=x+9, g(x)=x^2-4x, h(x)=x^4+2x^3

what is the degree of (f×g×h)(x)?

a)7
b)8
c)21
d)24​

Answer 1

The answer is 8

Explanation:

Answer 2

The degree of (f × g × h)(x) is 7.

i.e option a ) 7

Explanation:

Given:

`f(x)=(x+9)\\\\g(x)=(x^(2) -4x)\\\\h(x)=(x^(4)+2 x^(3))`

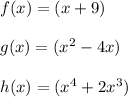
To Find:

Degree of (f × g × h)(x) = ?

Solution:

For multiplication of given function we require

Law of indices:

`(x^(a) )(x^(b) )=x^((a+b))`

Distributive Property:

(A + B)(C + D) = A (C + D) + B(C +D)

= AC + AD + BC +BD

Now,

`(f* g* h)(x) = (x+9)(x^(2) -4x)(x^(4) +2x^(3))\\ \\ =(x(x^(2) -4x) + 9(x^(2) -4x))(x^(4) +2x^(3))\\\\=(x^(3)+5x^(2)-36x)(x^(4) +2x^(3))\\\\=x^(7)+5x^(6)-36x^(5)+2x^(6)+10x^(5)-72x^(4)\\\\=x^(7) +7x^(6)-26x^(5)-72x^(4) \\\\\therefore (f* g* h)(x) = x^(7) +7x^(6)-26x^(5)-72x^(4)`

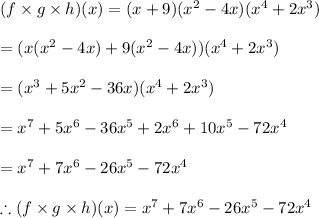
Degree is highest power raised to the variable.

Therefore here highest power raised to the variable is 7

Therefore degree of (f × g × h)(x) is 7.