Question

St lies on the coordinate plane with s located at (3.2). The midpoint of dt is z(3,9) can the location of t be determined? It so, state the location. If not, explain why not

Answer 1

I think your question in correct way is like this:

ST lines on the coordinate plane with S located at (3,2). The midpoint of ST is Z(3,9). Can the location of T be determined? If so, state the location. If not, explain why not.

Answer:

T(3,16)

Explanation:

If two points A(
`x_(a)`,
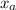`y_(a)`) and B(
`x_(b)`,
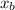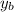`y_(b)`) are given then the coordinate of midpoint of AB is given by M(
`(x_(a)+x_(b))/(2)`,
`(y_(a)+y_(b))/(2)`).

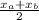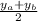Similarly coordinates of Z in terms of coordinates of S and T is given by:

`x_(z)=(x_(s)+x_(t))/(2)\\3=(3+x_(t))/(2)\\6=3+x_(t)\\ \therefore x_(t)=3`

`y_(z)=(y_(s)+y_(t))/(2)\\9=(2+y_(t))/(2)\\18=2+y_(t)\\ \therefore y_(t)=16`

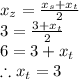
Therefore, point T is located at (3,16).