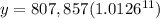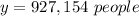Answer:
Explanation:
we have a exponential function of the form
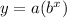
where
y is the population of San Francisco
x is the number of years
a is the initial population
b is the base
r is the rate of grown
b=(1+r)
In this problem we have

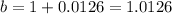
ordered pair (6, 870,887)
substitute in the exponential function
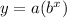
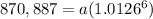
Solve for a
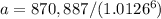
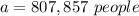
so
The exponential function is equal to
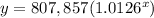
In 5 more years the number of years will be equal to
6+5=11 years
For x=11 years
substitute the value of x in the exponential function and solve for y