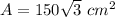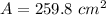Question

Find the area of the regular polygon. Round to the nearest tenth.

Answer 1

`A=259.8\ cm^2`

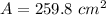
Explanation:

we know that

The figure represent a regular hexagon

A regular hexagon can be divided into six congruent equilateral triangles

Let

b ---> the length side of the regular hexagon

see the attached figure to better understand the problem

`cos(30\°)=(5√(3))/(b)`

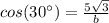
Remember that

`cos(30\°)=(√(3))/(2)`

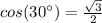
so

`(5√(3))/(b)=(√(3))/(2)\\\\b=10\ cm`

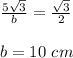
Find the area of the regular hexagon

The area of a regular hexagon is equal to the area of six congruent equilateral triangles

`A=6[(1)/(2)(b)(h)]`

we have

`b=10\ cm`

`h=5√(3)\ cm`

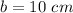
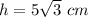
substitute

`A=6[(1)/(2)(10)(5√(3))]`

`A=150√(3)\ cm^2`

`A=259.8\ cm^2`