Question

A tank whose bottom is a mirror is filled with water to a depth of 20.0 cm. A small fish floats motionless 7.0 cm under the surface of the water. (a) What is the apparent depth of the fish when viewed at normal incidence? (b) What is the apparent depth of the image of the fish when viewed at normal incidence?

Answer 1

The apparent depth of (a) the fish is 5.3 cm and (b) the image of the fish is 24.8 cm.

Step-by-step explanation:

According to the following equation:

`(n_(w) )/(s) +(n_(a) )/(s') = (n_(a)- n_(w))/(R_(c) ) \\`

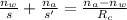
where nw and na is the refractive indices of water (1.33) and air (1.00) respectively; s is the depth of the fish below the surface of the water; s' is the apparent depth of the fish from normal incidence and Rc is the radius of curvature of the mirror at the bottom of the tank.

Note that the bottom of the tank is assumed to be a flat mirror, therefore the radius of curvature is very large (R⇒∞).

Therefore, the above equation can be expressed as:

`(n_(w))/(s) +(n_(a))/(s')=0`

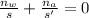
Now we can solve for the apparent depth of the fish.

(a)
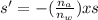`s'=-((n_(a))/(n_(w)))x s` (Make s' subject of the formula from the above equation)

`s'=((1.00)/(1.33) )x7cm`

∴
`s'=5.3 cm.`

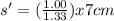
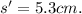
(b) The motionless fish floats 13 cm above the mirror, therefore the image of the fish will be situated at 13 + 20 =33 cm away from the real fish.

Therefore, s = 33 cm

`s'=-((n_(a))/(n_(w)))x s`

`s'=((1.00)/(1.33) )x 33 cm`

`s'=24.8 cm.`

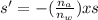
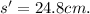
NB: Here, it is assumed that the water is pure, as impurities may alter the refractive index of water.