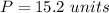Question

The coordinates of the vertices of a polygon are (-2, 1). (-3, 3), (-1, 5), (2, 4), and (2, 1). What is the perimeter of the polygon to the nearest tenth of a unit.

Do not label your answer. Answer with a number only.

Answer 1

`15.2\ units`

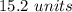
Explanation:

step 1

Plot the vertices of the polygon to better understand the problem

we have

`A(-2, 1). B(-3, 3), C(-1, 5), D(2, 4),E(2, 1)`

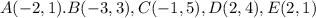
using a graphing tool

The polygon is a pentagon (the number of sides is 5)

see the attached figure

The perimeter is equal to

`P=AB+BC+CD+DE+AE`

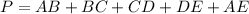
the formula to calculate the distance between two points is equal to

`d=\sqrt{(y2-y1)^(2)+(x2-x1)^(2)}`

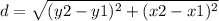
step 2

Find the distance AB

`A(-2, 1). B(-3, 3)`

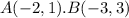
substitute in the formula

`d=\sqrt{(3-1)^(2)+(-3+2)^(2)}`

`d=\sqrt{(2)^(2)+(-1)^(2)}`

`d_A_B=√(5)=2.24\ units`

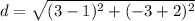
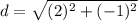
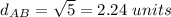
step 3

Find the distance BC

`B(-3, 3), C(-1, 5)`

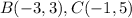
substitute in the formula

`d=\sqrt{(5-3)^(2)+(-1+3)^(2)}`

`d=\sqrt{(2)^(2)+(2)^(2)}`

`d_B_C=√(8)=2.83\ units`

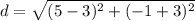
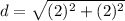
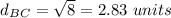
step 4

Find the distance CD

`C(-1, 5), D(2, 4)`

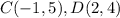
substitute in the formula

`d=\sqrt{(4-5)^(2)+(2+1)^(2)}`

`d=\sqrt{(-1)^(2)+(3)^(2)}`

`d_C_D=√(10)=3.16\ units`

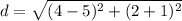
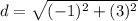
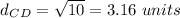
step 5

Find the distance DE

`D(2, 4),E(2, 1)`

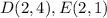
substitute in the formula

`d=\sqrt{(1-4)^(2)+(2-2)^(2)}`

`d=\sqrt{(-3)^(2)+(0)^(2)}`

`d_D_E=√(9)\ units`

`d_D_E=3\ units`

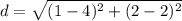
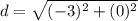
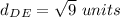
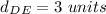
step 6

Find the distance AE

`A(-2, 1).E(2, 1)`

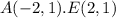
substitute in the formula

`d=\sqrt{(1-1)^(2)+(2+2)^(2)}`

`d=\sqrt{(0)^(2)+(4)^(2)}`

`d_A_E=√(16)\ units`

`d_A_E=4\ units`

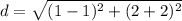
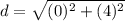
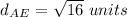
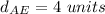
step 7

Find the perimeter

`P=AB+BC+CD+DE+AE`

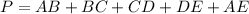
substitute the values

`P=2.24+2.83+3.16+3+4=15.23\ units`

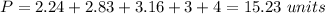
Round to the nearest tenth of a unit

`P=15.2\ units`