The coordinates of the midpoint of the segment joining the two points (0, 2) and (6, 4) is (3, 3)
Solution:
Given that two points are (0, 2) and (6, 4)
To find: coordinates of the midpoint of the segment joining the two points
The midpoint of line joining two points is given as:
For a line containing two points
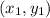 and
and
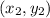
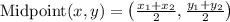
In the given sum, two points are (0, 2) and (6, 4)
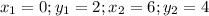
Substituting the values in given formula,
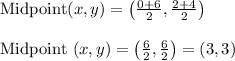
Thus the required midpoint is (3, 3)