Question

Evaluate the cumulative distribution function, F, for the given random variable, X, at specified values: also determine the requested probabilities. f(x) = (125/31) (1/5)^x, x = 1, 2, 3 Give exact answers in form of fraction. F(1) = ____________F(2) = __________F(3) =____________ (a) P(X lessthanorequalto 1.5) =____________(b) P(X lessthanorequalto 3) =___________(c) P(X > 2) =__________(d) P(1 < X lessthanorequalto 2) =______

Answer 1

Explanation:

Given that x is a random variable with probability density function given as

`f(x) =(125)/(31) *\(frac{1}{5} )^x, x=1,2,3`

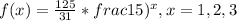
To find cumulative function for x

F(1) =
`f(1) = (125)/(31*5) =(25)/(31)`

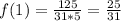
F(2) =
`f(1)+f(2)\\=(25)/(31) +(125)/(31)*(1)/(25)=(30)/(31)`

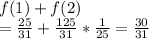
F(3) =
`f(1)+f(2)+f(3)\\= (30)/(31)+(125)/(31*125)\\=1`

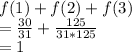
a) P(X lessthanorequalto 1.5)

=
`P(X\leq 1.5) = F(1)\\=(25)/(31)`

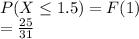
(b) P(X lessthanorequalto 3) =__F(3) = 1_________

(c) P(X > 2) =__f(3) = 1/31________

(d) P(1 < X lessthanorequalto 2) =__f(2) = 25/31____