Answer:
distance = 9.495 mm
Explanation:
Given data
slits distance = 0.100 mm
viewing screen distance = 1.50 m
wavelength = 633 nm
to find out
how far apart are the bright fringes on the viewing screen
solution
we use here double slit diffraction condition that is
d sin(θ) = m λ .......................1
here m = 0, 1 , 2 , 3 .....
and here for θ small so
sin(θ) = tan(θ) =
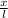
so x = l sin (θ)
so from equation 1
x =
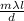
and
x1 =
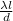 ...............2
...............2
x2 =
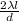 ..............3
..............3
so distance x2 - x1 will be
distance =
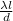
distance =
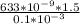
distance = 9.495 mm