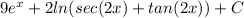Question

Find the most general antiderivative of the function. (Check your answer by differentiation. Use C for the constant of the antiderivative.)f(x) = 9ex + 4 sec2x

Answer 1

`\int\ {f(x)} \, dx = 9e^x + 2ln(sec(2x) + tan(2x)) + C`

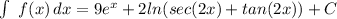
Explanation:

think of the function having two parts,
`9e^x` and
`4sec(2x)`

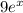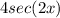
and integrate them separately.

• First integrate
  `9e^x`

`\int\ {9e^x} \, dx \\`

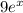
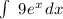
since 9 is a constant you

`9\int\ {e^x} \, dx\\`

`9e^x`

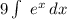
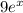
• Next integrate
  `4sec(2x)`

`\int\ {4sec(2x)} \, dx \\4\int\ {sec(2x)} \, dx \\`

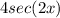
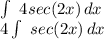
we can use u-substitution
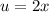`u = 2x` and
`du =2dx`

`4\int\ {sec(u)} \, (du)/(2) \\2\int\ {sec(u)} \, du\\`

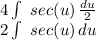
think of it as only integrating sec(x)

`2(ln(sec(u) + tan(u)))\\2(ln(sec(2x) + tan(2x)))\\`

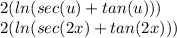
• Now combine the two answers and include the constant of integration (+C)

Answer::
`9e^x + 2ln(sec(2x) + tan(2x)) + C\\`