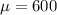Question

Rachael got a 550 on the analytical portion of the Graduate Record Exam (GRE). If GRE scores are normally distributed and have mean μ = 600 and standard deviation σ = 25, what is her standardized score?

Answer 1

Z=-2

This value means that the score of Rachel 550 it's 2 deviations below the mean of the population
`\mu=600`

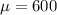
Explanation:

1) Previous concepts

Normal distribution, is a "probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean".

The Z-score is "a numerical measurement used in statistics of a value's relationship to the mean (average) of a group of values, measured in terms of standard deviations from the mean".

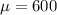`\mu=600` represent the population mean for the Graduate Record Exam (GRE)

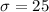`\sigma=25` represent the population standard deviation for Graduate Record Exam (GRE)

2) Solution to the problem

Let X the random variable that represent the Graduate Record Exam (GRE) of a population, and for this case we know the distribution for X is given by:

`X \sim N(600,25)`

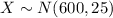
Where
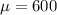`\mu=600` and
`\sigma=25`

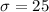
We want to find the z score for a score of 550. And in order to do this we need to apply the formula for the z score given by:

`z=(x-\mu)/(\sigma)`

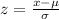
If we apply this formula to our probability we got this:

`z=(550-600)/(25)=-2`

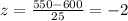
So the answer for our case would be Z=-2

This value means that the score of Rachel 550 it's 2 deviations below the mean of the population
`\mu=600`