Question

If the perimeter of square region S and the perimeter of rectangular region R are equal and the sides of R are in the ratio 2:3 then the ratio of the area of R to the area of S

A. 25:16
B. 24:25
C. 5:6
D. 4:5
E. 4:9

Answer 1

Answer: The correct option is (B) 24 : 25.

Step-by-step explanation: Given that the perimeter of square region S and the perimeter of rectangular region R are equal and the sides of R are in the ratio 2 : 3.

We are to find the ratio of the area of R to the area of S.

Let 2x, 3x be the sides of rectangle R and y be the side of square S.

Then, according to the given information, we have

`\textup{Perimeter of rectangle R}=\textup{Perimeter of square S}\\\\\Rightarrow2(2x+3x)=2(y+y)\\\\\Rightarrow 5x=2y\\\\\Rightarrow (x)/(y)=(2)/(5)~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(i)`

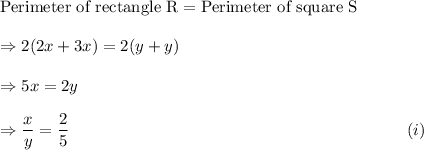
Therefore, the ratio of the area of R to the area of S is

`(2x*3x)/(y* y)\\\\\\=(5x^2)/(y^2)\\\\\\=6\left((x)/(y)\right)^2\\\\\\=6*\left((2)/(5)\right)^2~~~~~~~~~~~[\textup{Using equation (i)}]\\\\\\=(24)/(25)\\\\=24:25.`

Thus, the required ratio of the area of R to the area of S is 24 : 25.

Option (B) is CORRECT.