Question

For which function is f(x) equal to f^1(x) ( answer choices in picture )

Answer 1

C.
`f(x)=(x+1)/(x-1)`

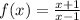
Explanation:

Let's find the inverse of each of the given options.

Option A:

`f(x)=(x+6)/(x-6)\\y=(x+6)/(x-6)`

To find
`f^(-1)(x)`, replace 'x' with 'y' and 'y' with 'x'. This gives,

`x=(y+6)/(y-6)`

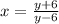
Rewrite in terms of 'y'. This gives,

`x(y-6)=y+6\\xy-6x=y+6\\xy-y=6x+6\\y=(6x+6)/(x-1)`

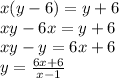
The given function
`y=(6x+6)/(x-1)\\e y=(x+6)/(x-6)`

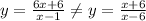
So, option A is incorrect.

Option B:

`f(x)=(x+2)/(x-2)\\y=(x+2)/(x-2)`

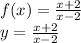
To find
`f^(-1)(x)`, replace 'x' with 'y' and 'y' with 'x'. This gives,

`x=(y+2)/(y-2)`

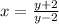
Rewrite in terms of 'y'. This gives,

`x(y-2)=y+2\\xy-2x=y+2\\xy-y=2x+2\\y=(2x+2)/(x-1)`

The given function
`y=(2x+2)/(x-1)\\e y=(x+2)/(x-2)`

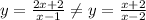
So, option B is incorrect.

Option C:

`f(x)=(x+1)/(x-1)\\y=(x+1)/(x-1)`

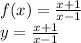
To find
`f^(-1)(x)`, replace 'x' with 'y' and 'y' with 'x'. This gives,

`x=(y+1)/(y-1)`

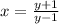
Rewrite in terms of 'y'. This gives,

`x(y-1)=y+1\\xy-x=y+1\\xy-y=x+1\\y=(x+1)/(x-1)`

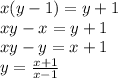
The given function
`y=(x+1)/(x-1)\ equals\ y=(x+1)/(x-1)`

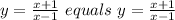
So, option C is correct.

Option D:

`f(x)=(x+5)/(x-5)\\y=(x+5)/(x-5)`

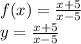
To find
`f^(-1)(x)`, replace 'x' with 'y' and 'y' with 'x'. This gives,

`x=(y+5)/(y-5)`

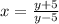
Rewrite in terms of 'y'. This gives,

`x(y-5)=y+5\\xy-5x=y+5\\xy-y=5x+5\\y=(5x+5)/(x-1)`

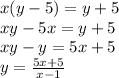
The given function
`y=(5x+5)/(x-1)\\e y=(x+6)/(x-6)`

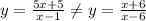
So, option D is incorrect.

Therefore, only option C is correct.