Answer:
Angular acceleration,
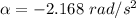
Step-by-step explanation:
Given that,
Number of revolution,
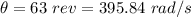
Diameter of the car, d = 0.88 m
Radius, r = 0.44 m
Initial speed of the car, u = 91 km/h = 25.27 m/s
Initial angular speed,
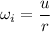
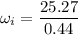

Final speed of the car, v = 63 km/h = 17.5 m/s
Final angular speed,
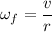
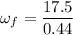
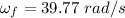
To find,
The angular acceleration of the tires.
Solution,
The angular acceleration of the wire can be calculated using third equation of kinematics as :
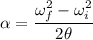

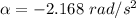
So, the angular acceleration of the tires is
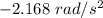 .
.