Question

If a snowball melts so that its surface area decreases at a rate of 3 cm2/min, find the rate at which the diameter decreases when the diameter is 9 cm.

Answer 1

Snow ball is melting with a rate of 0.265 cm per minute.

Explanation:

Snow ball is a sphere in shape, so surface area of the ball will be represented by the formula,

S = 4πr²

If snow ball is melting, then
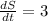`(dS)/(dt)=3` cm² per minute

We have to find the rate of decrease in the diameter of the snow ball when the radius of the ball is =
`(9)/(2)=4.5` cm

Now
`(dS)/(dt)=4\pi (d)/(dt)(r^(2))`

`3=4\pi (2r)(dr)/(dt)`

`3=4\pi (9)(dr)/(dt)`

`(dr)/(dt)=(3)/(36\pi)`

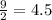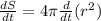
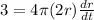
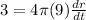
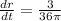
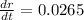`(dr)/(dt)=0.0265` cm per minute

Therefore, the snow ball is melting with a rate of 0.265 cm per minute.