Question

Find the quadratic function that passes through the points: (-1,6), (1,4), and (2,9).

y=ax²+bx+c

Answer 1

The quadratic function that passes through given points is y = 2 x² - x + 3 .

Explanation:

The given quadratic function as

y = a x² + b x + c

The equation passes through the points ( - 1 , 6 ) , ( 1 , 4 ) and ( 2, 9 )

As The points passes through equation then

At points ( - 1 , 6 )

6 = a (1)² + b ×( - 1 ) + c

Or, a - b + c = 6 .....A

Again At points ( 1 , 4 )

4 = a (1)² + b × 1 + c

Or, a + b + c = 4 .......B

Similarly At points ( 2 , 9 )

9 = a (2)² + b × 2 + c

Or, 4 a +2 b + c = 9 ....,,,C

Now solving equation A and B

( a - b + c ) + ( a + b + c ) = 6 + 4

Or, a + c =
`(10)/(2)`

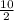
I.e a + c = 5 ......D

Similarly Solving equation B and C

( 4 a +2 b + c ) - 2 × ( a + b + c ) = 9 - 2 × 4

Or, ( 4 a - 2 a + 2 b - 2 b + c - 2 c ) = 9 - 8

Or, ( 2 a - c ) = 1 .....E

Solving D and E

( a + c ) + ( 2 a - c ) = 5 + 1

Or, 3 a = 6

∴ a =
`(6)/(3)`

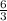
I.e a = 2

Put the value of a in Eq D

So , a + c = 5

Or, c = 5 - a

∴ c = 5 - 2 = 3

I.e c = 3

Put The value of a and c in Eq A

a - b + c = 6

Or, b = a + c - 6

Or . b = 2 + 3 - 6

∴ , b = 5 - 6

I.e b = - 1

Now, Putting the values of a , b , c in the given quadratic equation

I.e y = a x² + b x + c

Or, y = 2 x² + ( - 1 ) x + 3

∴ The quadratic eq is y = 2 x² - x + 3

Hence The quadratic function that passes through given points is y = 2 x² - x + 3 . Answer