Question

Melissa is looking for the perfect man. She claims that of the men at her college, 32% are smart. 33% are funny, and 16% are both smart and funny. Use the Venn diagram to answer the following question: If Melissa is right, what is the probability that a man chosen at random from her college is neither funny nor smart? a. 0.51 b. 0.84 c. 0.67 d. None of the given answers is correct. e. 0.35

Answer 1

a. 0.51

Explanation:

We solve this problem building the Venn's diagram of these probabilities.

I am going to say that:

A is the probability that a men is smart.

B is the probability that a men is funny.

C is the probability that a mean is neither of those.

We have that:

`A = a + (A \cap B)`

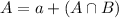
In which a is the probability that a men is smart but not funny and
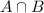`A \cap B` is the probability that a men is both of these things.

By the same logic, we have that:

`B = b + (A \cap B)`

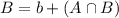
The sum of the probabilities is decimal 1, so:

`a + b + (A \cap B) + C = 1`.

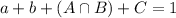We want to find C. We find the values of each of these probabilities, starting from the intersection.

16% are both smart and funny. This means that
`A \cap B = 0.16`

33% are funny. This means that
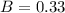`B = 0.33`. So

`B = b + (A \cap B)`

`0.33= b + 0.16`

`b = 0.17`.

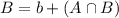
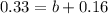
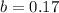32% are smart. This means that
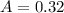`A = 0.32`. So

`A = a + (A \cap B)`

`0.32= a + 0.16`

`a = 0.16`.

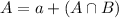
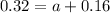
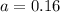Now we find C

`a + b + (A \cap B) + C = 1`

`0.16 + 0.17 + 0.16 + C = 1`

`0.49 + C = 1`

`C = 0.51`.

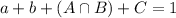
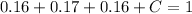
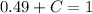
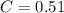The correct answer is:

a. 0.51