Question

A child is riding a merry-go-round, which has an instantaneous angular speed of 1.25 rad/s and an angular acceleration of 0.745 rad/s2. The child is standing 4.65 m from the center of the merry-go-round. What is the magnitude of the acceleration of the child?

Answer 1

8.04924 m/s²

Step-by-step explanation:

r = Distance the child is from the center = 4.65 m

`\alpha` = Angular acceleration = 0.745 rad/s²

`\omega` = Angular velocity = 1.25 rad/s

Velocity is given by

`v=r\omega\\\Rightarrow v=4.65* 1.25\\\Rightarrow v=5.8125\ m/s`

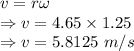
Radial acceleration is given by

`a_r=(v^2)/(r)\\\Rightarrow a_r=(5.8125^2)/(4.65)\\\Rightarrow a_r=7.265625\ m/s^2`

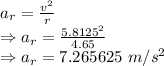
Tangential acceleration is given by

`a_t=\alpha r\\\Rightarrow a_t=0.745* 4.65\\\Rightarrow a_t=3.46425\ m/s^2`

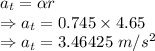
The resultant acceleration is given by

`a=√(a_r^2+a_t^2)\\\Rightarrow a=√(7.265625^2+3.46425^2)\\\Rightarrow a=8.04924\ m/s^2`

The magnitude of the acceleration of the child is 8.04924 m/s²