Question

The shape of a dome can be

modeled by the equation h =
- 2d^2 + 100 where h is the height
(in feet) of the dome from the
floor d feet from its center. How
far from the center of the dome
is the height 50 feet?

Answer 1

5 feet

Explanation:

We are told that the height of the dome can be modelled by the equation:

`\boxed{h = -2d^2 + 100}`

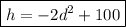
The question is essentially asking us: for what value of d will the value of h be 50 feet?

To solve this, we have to substitute h in the equation with 50 and then solve for d.

∴
`50 = -2d^2 + 100`

⇒
`50 + 2d^2 + 100`

⇒
`2d^2 = 100 - 50`

⇒
`d^2 = (100 - 50)/(2)`

⇒
`d^2 = 25`

⇒
`d = √(25)`

⇒
`d = \bf 5`

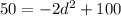
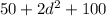
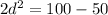
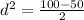
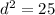
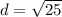
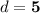
This means that 5 feet from the center of the dome, the height of the dome is 50 feet.