Answer:
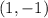 and
and
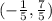
In decimal form this would be (1, -1) and (-0.2, 1.4)
Explanation:
Basically here we are trying to solve a system of 2 equations. The first one is a straight line and the second is a circle. This can be done graphically and graph is attached. There will be two points where the line cuts the circle so two solution sets
The equations are
Line Equation
 (1) and
(1) and
Circle Equation
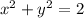 (2)
(2)
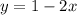
Plug this value of y into the second equation for the circle
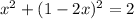
Apply the perfect squares formula
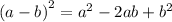
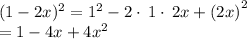
So equation (2) becomes

Solve using the quadratic formula
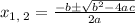
Here a is the coefficient of x ², b is the coefficient of x and c is the constant
So
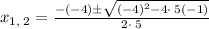
Now,
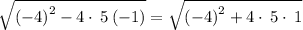
=
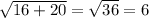
Therefore
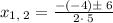
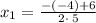 =
=
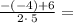
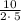


 =
=
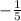
To find corresponding values for
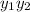 plug these values of
plug these values of
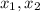 into the line equation
into the line equation
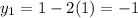
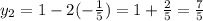
So the two points of intersection are
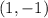 and (
and (
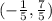 .
.
In decimal form this would be (1, -1) and (-0.2, 1.4)
See attached graph