Answer:
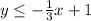
Explanation:
The equation of the line is y = mx + b
where
m is the slope = rise/run
b = y-intercept ie where the line crosses the y-axis at x = 0
The line crosses the y axis at y = 1 so the y-intercept is 1 and the point at which the line crosses is (0, 1)
We have the equation as
y = mx + 1
To find the slope, take any two points on the line. Find the corresponding difference in the y values and divide this difference by the corresponding difference in the x values
Two convenient points are (0, 1) and (3, 0)
Slope =
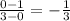
Equation of the line :
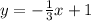
To find out if the inequality in the shaded region is a ≥ or a ≤ inequality, take a point in the shaded region. Determine whether the chosen point x, y values satisfy which of the following equations
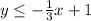 (1)
(1)
or
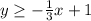 (2)
(2)
The point (0,0) is inside the shaded region
Plug in these values into inequality (1)
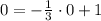 = 1
= 1
Is 0 ≤ 1 ?
Indeed it is so the inequality is
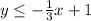 (Answer)
(Answer)
The region on the opposite side of the line must be a ≥ inqeuality
The attached graph makes it clearer