Question

A medical resident is convinced that, on average, residents at his hospitals work for over 3 hours more per week than residents at other hospitals. Suppose that he finds that a random sample of 30 residents at his hospital works an average of 74.3 hours per week with a standard deviation of 2.6 hours. He also surveys a random sample of 30 residents working at other hospitals and finds they worked an average of 70.1 hours per week with a standard deviation of 2.9 hours. Do the data support the resident’s belief? Test the relevant hypotheses at a significance level of 0.05.

Answer 1

At 0.05 significance level, there is significant evidence that residents at the medical resident's hospitals work for over 3 hours more per week than residents at other hospitals.

Explanation:

`H_(0)`:residents at the medical resident's hospitals work for 3 hours more per week than residents at other hospitals

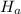`H_(a)`:residents at the medical resident's hospitals work for over 3 hours more per week than residents at other hospitals.

Test statistic can be calculated using the formula:

z=
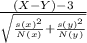`\frac{(X-Y)-3}{\sqrt{(s(x)^2)/(N(x))+(s(y)^2)/(N(y))}}` where

• X is the average working hours at the medical resident's hospitals (74.3)

• Y is the average working hours at other hospitals (70.1)

• s(x) is the sample standard deviation of working hours of the resident's hospitals (2.6)

• s(y) is the sample standard deviation of working hours of the other hospitals (2.9)

• N(x) is the sample size of working hours of the resident's hospitals (30)

• N(y) is the sample size of working hours of the other hospitals(30)

z=
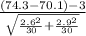`\frac{(74.3-70.1)-3}{\sqrt{(2.6^2)/(30)+(2.9^2)/(30)}}` ≈ 1.6875

P-value of the test statistic is 0.046. Since 0.046>0.05 we reject the null hypothesis.