Answer: After 18.05 minutes, the temperature of steel becomes 100 degrees.
Explanation:
Since we have given that
Initial temperature = 2500
At t = 0,
we get that
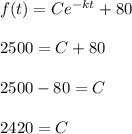
After 2 minutes, the temperature of the steel is 1500 degrees.
so, it becomes,
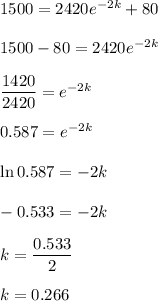
So, We need to find the number of minutes when the temperature of steel would be 100 degrees.
So, it becomes,
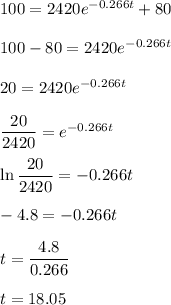
Hence, after 18.05 minutes, the temperature of steel becomes 100 degrees.