Question

An iron bar is heated. Its length, L, in millimetres can be modelled by a linear function, L= mT + c,

where T is the temperature measured in degrees Celsius (°C).


At 150°C the length of the iron bar is 180 mm.

Answer 1

L=1.44T

Explanation:

We can determine c by knowing the lenght L and the temperature T which is given. We can determine c:

`L=180=m\cdot{150}+c[/tex}</p><p>[tex]180-m\cdot{150}=c`

We can take any point to determine m, we can determine this by the ratio of length to temperature:

`=180/150=1.2`

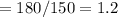
We know now that the lenght is 1.2 times the temperature. IF the the temperature is 50, the length is:

`=50x1.2=60`

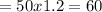
m is the gradient defined as (L2-L1)/(T2-T1) and we have all the terms:

[tex]m=(180-50)/(150-60)=130/90=1.44{tex]

We solve c by L=0:

c = 0