Question

A pulley of radius 10cm turns at 6 revolutions per second. What is the linear velocity of the belt driving the pulley in meters per second?

1.67 m/s
3.77 m/s
376.99 m/s
166.67 m/s

Answer 1

v = 3.77 m/s

Explanation:

Uniform Circular Motion

It's a movement in which an object moves along the circumference of a circle. It can also be defined as a rotation along a circular path.

The angular speed can be calculated in two different ways:

`\displaystyle \omega=(v)/(r)`

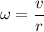
Where:

v = tangential or linear speed

r = radius of the circle described by the rotating object

Also:

`\omega=2\pi f`

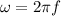
Where:

f = frequency

The frequency is calculated when the number of revolutions n and the time t are known:

`\displaystyle f=(n)/(t)`

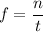
The pulley turns at n=6 revolutions per t= 1 second, thus:

`\displaystyle f=(6)/(1)`

f = 6 Hz

The angular speed is:

`\omega=2\pi 6`

`\omega=37.7 \ rad/s`

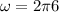
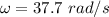
The linear speed can be calculated by solving the first equation for v:

`v = \omega\cdot r`

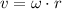
The radius is converted to meters: r=10 cm = 0.1 m. Calculate the speed:

`v = 37.7 \ rad/s\cdot 0.1\ m`

v = 3.77 m/s