Question

Listed below are measured amounts of caffeine? obtained in one can from each of 14 brands. Find the? range, variance, and standard deviation for the given sample data. Include appropriate units in the results [mg per 12oz drink; (mg per 12oz of drink)2; brands2; brands]. Are the statistics representative of the population of all cans of the same 14 brands? consumed?

31
52
35
57
0
32
35
52
46
41
30
41
0
0

Answer 1

Range is 57.

Variance is 375.143.

standard deviation is 19.37.

Explanation:

Consider the provided information.

Range is the difference between highest and lowest data value.

The highest data value is 57 and lowest is 0.

Thus the range is 57-0=57

Range is 57.

Mean is the sum of data value divided by the number of data value:

`\bar x=(31+52+35+57+0+32+35+52+46+41+30+41+0+0)/(14)\approx32.286`

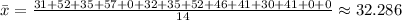
The variance is the sum of squared deviation from the mean divided by n-1.

`s^2 =(\sum(x_i -\bar x)^2)/(n - 1)`

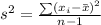
Substitute the respective values in the above formula we get:

`s^2=((31 - 32.286)^2 +(52-32.286)^2+ ... + (0 -32.286)^2)/(14 - 1)\approx 375.143`

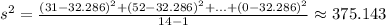
Hence, the variance is 375.143.

Standard deviation is square root of variance.

standard deviation =
`√(375.143)`

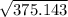
standard deviation ≈ 19.37

Hence, standard deviation is 19.37.

For all cans consumed, the statistics are not representative of the population because in the calculations each brand is weighted equally. Each of the 14 brands of soda is unlikely to be consumed in the same way.

It is very unlikely that all 14 drinks are consumed equally. So,given data is not representative of population