Question

The equation of motion for a simple harmonic oscillator (SHO) is:

m(d2x/ dt2) = −kx
where m is the mass and k the spring constant. A generic solution of the above differential equation can be written in the form:
x(t) = A cos(ωt + φ0).
Where ω = p k/m and A and φ0 are arbitrary constants to be determined by the initial conditions of the motion. You are given the following information: a block of mass m = 10 kg is attached to a spring with spring constant k = 2.5N/m; at time t = 0 the amplitude of the motion is 0, and the velocity is -5 m/s.
(a) Using the generic solution (1) above find the form x(t) for the position as a function of time for the block (you need to determine the constants A, ω and φ0). Do not forget to write clearly the appropriate dimension for each quantity, A, φ0, ω.
(b) Plot the function x(t) that you found in part (a) from t = 0 until t = 20s.
(You can use a graphical calculator or WolframAlpha or Desmos to make your plot)

Answer 1

Step-by-step explanation:

ω =
`\sqrt{(k)/(m) }`

k = 2.5 N/m

m = 10 kg

`\omega = \sqrt{(2.5)/(10) }`

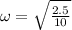
ω = .5 rad /s

x(t) = A cos(ωt + φ₀)

When t = 0 , x(t) = 0

0 = A cos(ωx 0 + φ₀)

cos φ₀ = 0

φ₀ = π /2

x(t) = A cos(ωt +π /2 )

Putting the value of ω

x(t) = A cos(.5 t +π /2 )

Differentiating on both sides

dx(t)/dt = - .5 A sin(.5 t +π /2 )

v(t) = - .5 A sin(.5 t +π /2 )

Given t =0 , v(t) = -5 m/s

-5 = - .5 A sin(.5 x0 +π /2 )

-5 = - .5 A sinπ /2

A = 10 m

x(t) = 10 cos( .5 t +π /2 )

b )

when t = π ( 3.14 s )

x(t) = - 10 m

when t = 2π ( 6.28s )

x(t) = 0

when t = 3π ( 9.42 s )

x(t) = 10 m

and so on