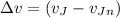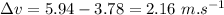Question

Two kids are playing on a newly installed slide, which is 3 m long. John, whose mass is 30 kg, slides down into William (20 kg), who is sitting at the very bottom end, and whom he holds onto when he arrives. Laughing, John & William leave the slide horizontally and land in the muddy ground near the foot of the slide. (A) If John starts out 1.8 m above William, and the slide is essentially frictionless, how fast are they going when they leave the slide? (B) Thanks to the mud he acquired, John will now experience an average frictional force of 105 N as he slides down. How much slower is he going when he reaches the bottom than when friction was absent?

Answer 1

`v=3.564\ m.s^(-1)`

`\Delta v =2.16\ m.s^(-1)`

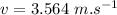
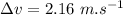
Step-by-step explanation:

Given:

• mass of John,
  `m_J=30\ kg`

• mass of William,
  `m_W=30\ kg`

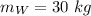
• length of slide,
  `l=3\ m`

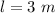
(A)

height between John and William,
`h=1.8\ m`

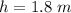
Using the equation of motion:

`v_J^2=u_J^2+2 (g.sin\theta).l`

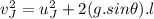
where:

v_J = final velocity of John at the end of the slide

u_J = initial velocity of John at the top of the slide = 0

Now putting respective :

`v_J^2=0^2+2* (9.8* (1.8)/(3))* 3`

`v_J=5.94\ m.s^(-1)`

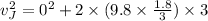
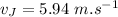
Now using the law of conservation of momentum at the bottom of the slide:

Sum of initial momentum of kids before & after collision must be equal.

`m_J.v_J+m_w.v_w=(m_J+m_w).v`

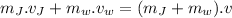
where: v = velocity with which they move together after collision

`30* 5.94+0=(30+20)v`

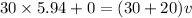
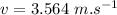`v=3.564\ m.s^(-1)` is the velocity with which they leave the slide.

(B)

• frictional force due to mud,
  `f=105\ N`

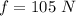
Now we find the force along the slide due to the body weight:

`F=m_J.g.sin\theta`

`F=30* 9.8* (1.8)/(3)`

`F=176.4\ N`

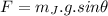
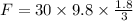
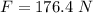
Hence the net force along the slide:

`F_R=71.4\ N`

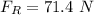
Now the acceleration of John:

`a_j=(F_R)/(m_J)`

`a_j=(71.4)/(30)`

`a_j=2.38\ m.s^(-2)`

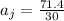
Now the new velocity:

`v_J_n^2=u_J^2+2.(a_j).l`

`v_J_n^2=0^2+2* 2.38* 3`

`v_J_n=3.78\ m.s^(-1)`

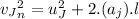
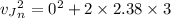
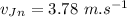
Hence the new velocity is slower by

`\Delta v =(v_J-v_J_n)`

`\Delta v =5.94-3.78= 2.16\ m.s^(-1)`