Question

Please Help me with this problem!!!

Answer 1

The total displacement of the object was 7.5 meters.

Step-by-step explanation:

There's a relation between the common movement analysis graphs that we can always use. These relations are the following:

The derivative (slope) of a displacement vs. time graph gives you the function of speed vs. time. Also, when you take the speed vs. time graph and find its derivative, you will get the acceleration function of the observed body.

Now, doing to opposite of derivation (integration), we are able to calculate the displacement of an object when we integrate the function of velocity vs. time. This is not a complicated process when we have a linear function, because integration is just calculating the area under the curve or line of a graph.

In this case, the graph forms a right triangle with the x axis, therefore, we are able to calculate displacement by finding the area under the line of the graph. It could also be made with integration, we are going to do it with both processes as they are both used, and in some cases you have to strictly use one of the 2 in order to get the most precise answers.

Method 1. By finding the area through geometry.

When we observe the line, we can crearly tell that the area under the graph constitutes a right triangle. Hence, the area under the graph is given by the following formula:

`A=(bh)/(2)`

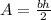
Substitute the values and calculate.

(Check attached image 1 to see where the values of b and h are taken from).

`A=((5)(3))/(2)\\ \\A=7.5`

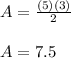
Hence, the total displacement of the object was 7.5 meters.

Method 2. By integration.

In this method, we'll need to find the equation of the line and then generate and solve a definite integral.

Take 2 points from the line.

(0, 0) and (5, 3).

Find the slope.

Formula:
`m=(y_(2) -y_(1) )/(x_(2)- x_(1) )`

`m=(3-0)/(5-0)= \\ \\m= (3)/(5)`

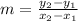
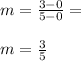
Find the equation of the line.

Formula:
`y-y_(1) =m(x-x_(1) )`

`y-(0) =(3)/(5) (x-(0) )\\ \\y=(3)/(5) x\\ \\`

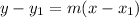
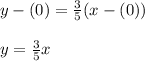
Integrate within the interval of interest (from 0 to 5).

`\int\limits^5_0 {((3)/(5) x)} \, dx \\ \\=(3)/(5) x^(2) *(1)/(2) \\ \\=(3)/(10) x^(2) \\\\ ((3)/(10) (5)^(2))-((3)/(10) (0)^(2))\\ \\((3)/(10) *25)-(0)\\ \\(75)/(10) \\ \\7.5`

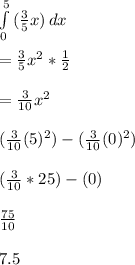
Once again, the total displacement of the object was 7.5 meters.