Question

This pair of figures is similar. Find the missing side. Help ASAP!!

Answer 1

The missing side “x” is 2.

Explanation:

From the given figure, we came to know that these are “similar triangles” where the ratio of the one “corresponding side” of a triangle is equal to the other two “corresponding sides” of a triangle.

Let the triangles be ∆ABC and ∆DEF

`\Delta A B C \sim \Delta D E F`

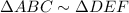
From similarity of triangle rule the sides,

`(A B)/(D E)=(B C)/(E F)`

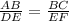
Given that,

AB = x, DE = 8, BC = 4 and EF = 16

`\text { Substitute the values in } (A B)/(D E)=(B C)/(E F) \text { to find }^(u) \mathrm{x}^(\prime \prime)`

`(x)/(8)=(4)/(16)`

`(x)/(8)=(1)/(4)`

`x=(8)/(4)`

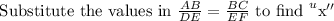
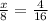
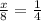
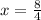
x = 2

Therefore, we found the missing side x = 2