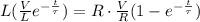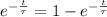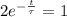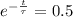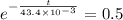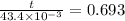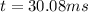Answer:30.08 ms
Step-by-step explanation:
Given
time Constant

Also rate at which energy is dissipated in the resistor equal to the rate at which energy is stored in inductor's magnetic Field
Energy stored in Inductor is
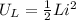
rate of Energy storing
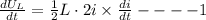
Rate of Energy dissipation from resistor i.e. Power is given by
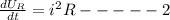
Equating 1 and 2
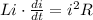
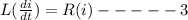
i is given by
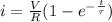
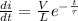
substitute the value of
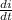 in 3
in 3