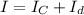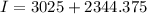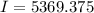Question

Consider a merry-go-round that has the form of a disc with radius 5.5 m and mass 155 kg. If five children, each of mass 20 kg, sit on the outer edge of the merry-go-round, what is the total moment of inertia?

Answer 1

`I=5369.375`

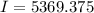
Step-by-step explanation:

Given:

• mass of merry go round,
  `M=155\ kg`

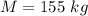
• radius of merry go round,
  `r=5.5\ m`

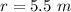
• mass of child,
  `m=20\ kg`

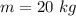
Considering merry-go-round as a disk, its moment of inertia is given as:

`I_d=(1)/(2) M.r^2`

`I_d=0.5* 155* 5.5^2`

`I_d=2344.375\ kg.m^2`

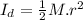
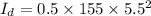
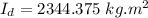
Considering children as point masses, their moment of inertia is given as:

`I_C=5(m.r^2)`

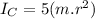
since there are 5 children

`I_C=5*20* 5.5^2`

`I_C=3025\ kg.m^2`

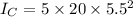
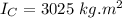
Now, total moment of inertia:

`I=I_C+I_d`

`I=3025+2344.375`

`I=5369.375`