Question

In rectangle abcd, diagonal ac, which is 20 inches in length

Answer 1

The question is incomplete. The complete question is attached below.

Answer:

(a). AB = 16.4 in

(b) BC = 11.5 in

Explanation:

From the rectangle ABCD shown below,

AB is the base of rectangle and CB is the altitude of the rectangle.

Given:

AC = 20 in

(a)

From triangle ABC,

Applying cosine ratio for angle 35°, we get:

`\cos(35)=(AB)/(AC)\\AB=AC* \cos(35)\\AB=20* \cos(35)=16.38\approx 16.4\ in`

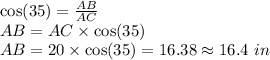
Therefore, AB = 16.4 in

(b)

Applying sine ratio for angle 35°, we get:

`\sin(35)=(CB)/(AC)\\CB=AC* \sin(35)\\AB=20* \sin(35)=11.47\approx 11.5\ in`

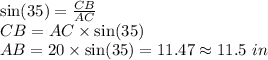
Therefore, CB = 11.5 in