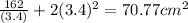Question

The base and sides of a container is made of wood panels. The container does not have a lid. The base and sides are rectangular. The width of the container is x cm . The length is double the width. The volume of the container is 54cm3 . Determine the minimum surface area that this container will have.

Answer 1

Minimum surface area =
`70.77 cm^2`

Explanation:

We are given that

Width of container=x cm

Length of container=2x cm

Volume of container=
`54 cm^3`

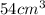
We have to find the minimum surface areas that this container will have.

Volume of container=
`l* b* h`

`x* 2x* h=54`

`2x^2h=54`

`h=(54)/(2x^2)=(27)/(x^2)`

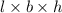
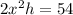
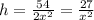
Surface area of container=
`2(b+l)h+lb`

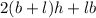
Because the container does not have lid

Surface area of container=
`S=2(2x+x)* (27)/(x^2)+2x* x`

`S=(162)/(x)+2x^2`

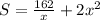
Differentiate w.r.t x

`(dS)/(dx)=-(162)/(x^2)+4x`

`(dx^n)/(dx)=nx^(n-1)`

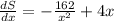
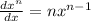
Substitute
`(dS)/(dx)=0`

`-(162)/(x^2)+4x=0`

`4x=(162)/(x^2)`

`x^3=(162)/(4)=40.5`

`x^3=40.5`

`x=(40.5)^{(1)/(3)}`

`x=3.4`

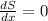
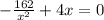
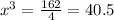
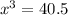
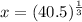
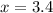
Again differentiate w.r.t x

`(d^2S)/(dx^2)=(324)/(x^3)+4`

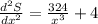
Substitute x=3.4

`(d^2S)/(dx^2)=(324)/((3.4)^3)+4=12.24>0`

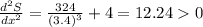
Hence, function is minimum at x=3.4

Substitute x=3.4

Then, we get

Minimum surface area =
`(162)/((3.4))+2(3.4)^2=70.77 cm^2`