Answer:
T = 8.19 s ,
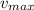 = 23 m / s
= 23 m / s
Step-by-step explanation:
In the simple harmonic motion the equation that describes them is
y = A cos wt
Acceleration can be found by derivatives
a = d²y / dt²
v = dy / dt = - Aw sin wt
a= d²y / dt² = - A w² cos wt
For maximum acceleration cosWT = + -1
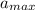 = -A w2
= -A w2
w = RA (
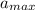 / A)
/ A)
w = RA (1.8 9.8 / 30.0)
w = 0.767 rad / s
The angular velocity is related to the frequency
w = 2π f
f = 1 / T
w = 2π / T
T = 2π / w
T = 2π / 0.767
T = 8.19 s
For maximum speed the sin wt = + -1
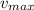 = A w
= A w
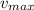 = 30.0 0.767
= 30.0 0.767
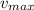 = 23 m / s
= 23 m / s