Question

Find the inequality represented by the graph.

Answer 1

f(x)<=-1/3x+1

Explanation:

so to test this you can do

0<=-1/3(0)+1

0<=1

so it's true

Answer 2

y
`\leq`
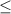
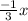`(-1)/(3)x` + 1

Explanation:

To find the inequality represented by the graph, we need to find the linear equation that represents the blue line.

As we can see, the:

y intercept: (0, 1)

x intercept: (3, 0)

So the slope of the equation is:

`m=(y_(2)-y_(1) )/(x_(2)-x_(1) )`

=
`(0-1)/(3-0)` =
`(-1)/(3)`

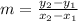
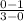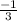
So use the slope and the slope-point formula, we find the linear expression

The standard form is: y = mx+ b

<=> y =
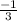`(-1)/(3)` x + b

Substitute the point (0, 1) to find b, we have:

b= y -
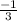`(-1)/(3)` x

<=> b= 1 - 0 =1

So the linear equation is: y =
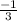`(-1)/(3)` x + 1

After that, we need to take a test point form the shaded area and evaluate the expression. Let the point be: (1, 2), we have:

2 =
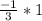`(-1)/(3) *1` +1

<=> 2=
`(2)/(3)`

We know that 2 >
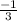`(-1)/(3)` this means that the left inequality sign is ≥ , so the inequality represented by the graph:

y
`\leq`
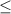
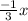`(-1)/(3)x` + 1