Question

A rubber ball filled with air has a diameter of 24.2 cm and a mass of 0.459 kg. What force is required to hold the ball in equilibrium immediately below the surface of water in a swimming pool? (Assume that the volume of the ball does not change. Indicate the direction with the sign of your answer.)

Answer 1

To solve this problem, it is necessary to apply the concepts related to Newton's second Law as well as to the expression of mass as a function of Volume and Density.

From Newton's second law we know that

F= ma

Where,

m = mass

a = acceleration

At the same time we know that the density is given by,

`\rho = (m)/(V) \rightarrow m = \rho V`

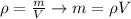
Our values are given as,

`g = 9.8m/s^2`

`m =0.459 kg`

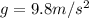
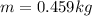
D=0.242 m

Therefore the Force by Weight is

`F_w = mg`

`F_w = 0.459kg * 9.8m/s^2 = 4.498N`

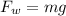
Now the buoyant force acting on the ball is

`F_B=\rho V g`

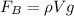
The value of the Volume of a Sphere can be calculated as,

`V = (4)/(3) \pi r^3`

`V =  (4)/(3) \pi (0.242/2)^3`

`V = 0.007420m^3`

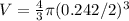
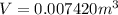
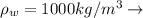`\rho_w = 1000kg/m^3 \rightarrow` Normal conditions

Then,

`F_B=0.007420*(1000)*(9.8) = 72.716 N`

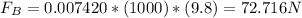
Therefore the Force net is,

`F_(net) = F_B -F_w`

`F_(net) = 72.716N - 4.498N =68.218 N`

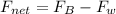
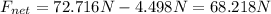
Therefore the required Force is 68.218N