Answer:
If the company produce and sell 'x' no. of thing-a-ma-bob , then
C(x) = $ (8809 + 2.05x)
R(x) = $ 4.92x
To make a profit the company must produce and sell at least 3070 thing-a-ma-bobs.
Explanation:
If the company produces and sells "x" no. of thing-a-ma-bob, then,
the cost function is given by,
C(x) = $ (8809 + 2.05x) ------------------------(1)
The revenue function is given by,
R(x) = $ 4.92x -------------------------------------(2)
If C(x) = R(x), then,
4.92x = 8809 + 2.05x
⇒ 2.87x = 8809
⇒ x =
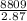
⇒ x
 3069.34
3069.34
So, to make a profit the company must produce and sell at least 3070 thing-a-ma-bobs.