Answer:
i. g = 70°
ii. x = 85°
Explanation:
Given:
Let first we name the triangle
i. ) Δ PQR , m∠ PRQ = 40°
ii. ) Δ ABC is a right angle at B and a line B- D-C
m∠ DAC = 25°
m∠ ACD = 60°
m∠ BDA = x°
To Find:
i. g = ?
ii. x = ?
Solution:
i.
In Δ PQR , PR ≅ QR ...........{Given]
∴ Δ PQR is an Isosceles Triangle.
c.........{ Base angles of Isosceles triangle are equal }
∴ m∠ PQR = m∠ RPQ = g
Now sum of all the angles in a triangle is 180°
∴ m∠ PQR + m∠ RPQ + m∠ PRQ = 180°....{Angle sum property of Triangle}
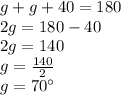
∴ g = 70°
ii.
We know sum of all the angles in a triangle is 180°
In Δ DAC
m∠ DAC + m∠ ACD + m∠ ADC = 180°.....{Angle sum property of Triangle}
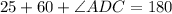
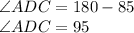
Now By Linear Pair Angle Property
m∠ ADB + m∠ ADC = 180° ........{Linear Pair Angle Property}
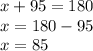
∴ x = 85°