Question

Suppose that F′(x)=f(x) and G′(x)=g(x). Which statements are true? A. If F and G differ by a constant, then f=g. B. If f and g differ by a constant, then F=G. C. If f=g, then F=G. D. None of the above

Answer 1

Answer: The correct option is

(A) If F and G differ by a constant, then f = g.

Step-by-step explanation: According to the given condition, we have

`F'(x)=f(x)~~~\textup{and}~~~G'(x)=g(x).`

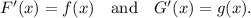
We are to select the correct statement.

Let F(x) = p(x) and G(x) = p(x) + c, c - constant.

Then, we get

`F'(x)=p'(x)~~~\textup{and}~~~G'(x)=p'(x).`

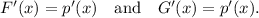
Therefore,

`F'(x)=G'(x)\\\\\Rightarrow f(x)=g(x)\\\\\Rightarrow f=g.`

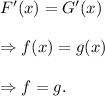
Thus, if F and G differ by a constant, then f = g.

Option (A) is CORRECT.