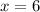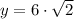Question

Find the values of x and y. Write your answers in simplest form

Answer 1

`x =6`

`y=6\cdot √(2)`

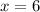
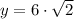
Explanation:

Trigonometric Ratios

The ratios of the sides of a right triangle are called trigonometric ratios. There are six trigonometric ratios: sine, cosine, tangent, cosecant, secant, and cotangent.

The longest side of the right triangle is called the hypotenuse and the other two sides are the legs.

Choosing any of the acute angles as a reference, it has an adjacent side and an opposite side. The trigonometric ratios are defined upon those sides.

The image shows a right triangle where the angle of 45° has x as the opposite leg, 6 as the adjacent leg, and y as the hypotenuse. The trigonometric ratio that applies here is the cosine ratio, defined as:

`\displaystyle \cos\theta=\frac{\text{adjacent leg}}{\text{hypotenuse}}`

`\displaystyle \cos 45^\circ=(6)/(y)`

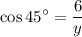
Solving for y:

`\displaystyle y=(6)/(\cos 45^\circ)`

`\cos 45^\circ=(√(2))/(2)=(1)/(√(2))`

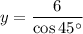
Substituting:

`\displaystyle y=(6)/((1)/(√(2)))`

`y=6\cdot √(2)`

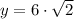
Now use the tangent ratio:

`\displaystyle \tan\theta=\frac{\text{opposite leg}}{\text{adjacent leg}}`

`\displaystyle \tan 45^\circ=(x)/(6)`

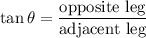
Solving for x:

`x=6\cdot\tan 45^\circ`

`\tan 45^\circ=1`

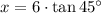
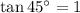
Substituting:

`x=6\cdot 1`

`x =6`

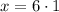
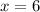
Answer:

`x =6`

`y=6\cdot √(2)`