Answer:
The maximum height of coin Jake tosses is 15 feet.
Explanation:
Given Jake tosses a coin up in the air
and the height of coin is model by h(t)=
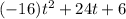
To find height of the coin when Jake tosses it:
When a coin is in the hand of Jake, time t=0
Height of coin is h(t)=
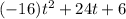
h(0)=
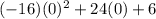
h(0)=6 feet.
Therefore, Height of coin at time t=0 is 6.
For maximum height of the coin,
h(t)=
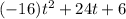
Differentiating both side,
![(d)/(dt)h(t)=(d)/(dt)[(-16)t^(2) +24t+6]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/pt4bgyn2u47hjkfm3v4cvik1wsl05g63bd.png)
![(d)/(dt)h(t)=(d)/(dt)[(-32)t+24]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/eapcqzw0l34bppycqp3o97b23qksb42kx4.png)
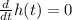
![(d)/(dt)[(-32)t+24]=0](https://img.qammunity.org/2020/formulas/mathematics/middle-school/jujlectjgprhbbstuujb6ozbknwl0q5lr5.png)
t=
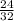
t=
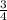
t=0.75
Now,
h(t)=
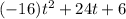
h(0.75)=
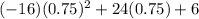
h(0.75)=15 feet.
The maximum height of coin jake tosses is 15 feet.