Question

The curved surface area of a cylinder is 880cm2 and its volume is 770cm3.Find its diameter and height.

Answer 1

The height of cylinder is: h = 80.07 cm

The diameter of cylinder is: d = 3.5 cm

Explanation:

Curved surface area of cylinder = 880 cm^2

Volume of cylinder = 770 cm^3

We need to find its diameter and height.

The formula used are:

`Curved\: surface\: area=2\pi rh\\Volume=\pi r^2h`

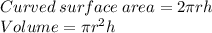
If we divide volume by curved surface, we can find radius

`(Volume)/(Curved\: surface\: area)=(\pi r^2h)/(2\pi rh) \\(770)/(880)=(r)/(2)\\0.875= (r)/(2)\\=> r= 0.875* 2\\r=1.75`

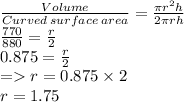
So, we get radius r = 1.75

Now, we can find height using curve surface area formula:

`Curved\: surface\: area=2\pi rh\\880=2(3.14)(1.75)h\\h=(880)/(10.99)\\h=80.07 \:cm`

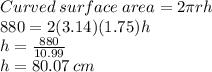
So, the height of cylinder is: h=80.07 cm

Now finding diameter using formula:
`d=2r`

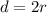
Putting value of r in above formula:

`d=2r\\d=2(1.75)\\d=3.5\:cm\\`

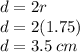
So, the diameter of cylinder is: d = 3.5 cm