Question

Please Help Quicly The equation 8x - 4y = 5 is dilated by a scale factor of 8 centered at the origin. What is the new slope and y-intercept after dilation?

Answer 1

For new line, slope m=2 and y-intercept c=(-10)

Explanation:

Note : Figure given is for reference to understand better.

Where redline is for given line and blueline for new line

The equation of given line 8x-4y=5 and it is dilated by a scale factor of 8 centered at the origin.

Step 1 : Find two points on given line.

When x=0, y=?

`8x-4y=5`

`8(0)-4y=5`

`y=(-5)/(4)`

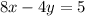
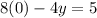
When y=0, x=?

`8x-4y=5`

`8x-4(0)=5`

`x=(5)/(8)`

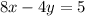
We get points
`A(0,(-5)/(4)), B((5)/(8),0)`

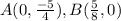
Step 2: Find distance from centered and scale it.

Now, It is said that line 8x-4y=5 dilated by a scale factor of 8 centered at the origin and point A and point B is on same.

So that point A and point B will also get dilated by a scale factor of 8 centered at the origin or distance of points from origin will be scaled by 8.

For point A:

Distance of point
`A(0,(-5)/(4))` from origin is
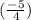`( (-5)/(4))` unit in x-direction and zero
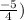`(-5)/(4))` unit in y-direction.

After scaled by factor of 8, the distance will multipy by 8 and new location is
`A'(0,-10)`

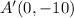
For point B:

Distance of point
`B((5)/(8),0)` from origin is
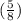`((5)/(8))` unit in x-direction and zero unit in y-direction.

After scaled by factor of 8, the distance will multipy by 8 and new location is
`B'(5,0)`

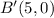
Step 3: Find Equation of new line.

Points
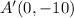`A'(0,-10)` and
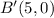`B'(5,0)` make a new line

The equation of given as

`(y-Y1)/(x-X1) = (Y2-Y1)/(X2-X1)`

`(y-(-10))/(x-0) = (0-(-10))/(5-0)`

`(y+(10))/(x) = 2`

`(y+(10))/(x) = 2`

`y+10= 2x`

`y= 2x-10`

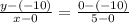
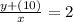
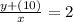
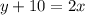
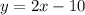
Now, Comparing with the equation of the line : y=mx + c

Where m=slope and c is the y-intercept

We get, Slope m=2 and y-intercept c=(-10)