Question

The Martian Colonies elect their government through a lottery. There are100,000 people living on Mars, and every year, a council of 99 co-equalleaders is randomly selected from the population. In how many ways canthe leadership be elected? Give your answer in terms of permutations orcombinations and explain your choice. You do not have to evaluate.

Answer 1

The answer is a 100,000-choose-99 (a combination.)

`P(100000, 99) = \displaystyle \left( \begin{array}{c}100000\cr 99\end{array}\right)`.

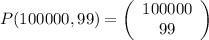Explanation:

A combination
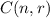`C(n, r)` or equivalently
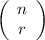`\displaystyle \left(\begin{array}{c}n \cr r\end{array}\right)` gives the number of ways to choose
`r` out of
`n` elements.

A permutation
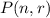`P(n, r)` also gives the number of ways to choose
`r` out of
`n` elements. On top of that, it accounts for the order of the elements. Two elements in different order counts twice in a permutation, but only once in a combination.

The question emphasize that the council members are "co-equal." That implies that the order of the members don't really matter. Hence a combination with
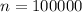`n = 100000` and
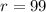`r = 99` would be a more suitable choice.