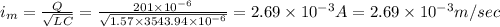Answer:
(a)1.57 kg
(b) 281.17 N/m
(c) 201 micrometer
(d)
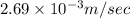
Step-by-step explanation:
We have given that value of inductor L = 1.57 Henry
Inductive energy
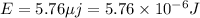
Maximum charge
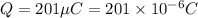
(A) In electrical mechanical system mass corresponds to inductance
So mass will be m = 1.57 kg
(B) We have given energy
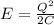
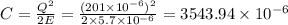
In electrical mechanical system spring constant is equivalent to
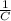
So spring constant
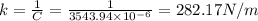
(c) Displacement is equivalent to maximum charge
So displacement will be
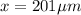
(d) Maximum speed is correspond to maximum current
As maximum current